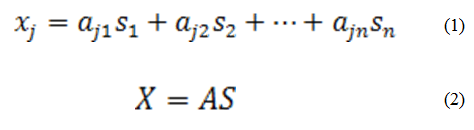Метод независимых компонент на Python

В процессе своей деятельности пришлось столкнуться с интересным математическим инструментом, называемым как Метод независимых компонент (МНК) или Анализ независимых компонент (АНК) (на английском Independent component analysis, ICA). Данный метод был предложен как способ решения задачи Слепого разделения сигналов или Слепого разделения источников (Blind source separation), то есть выделение независимых сигналов из предварительно смешанных данных.

Приведем пример — в чем заключается суть задачи Слепого разделения сигналов. Допустим у нас имеется два человека в одном помещении, которые что-то говорят / поют / пускают акустические волны и два микрофона в разных частях помещения, фиксирующие окружающие звуки. То есть на анализирующую систему от двух микрофонов у нас поступает два сигнала, каждый из которых представляет собой оцифрованную смесь двух акустических волн говорящих и каких нибудь шумов. Так вот цель решения задачи — выделить из поступающих смесей наши исходные сигналы.

Так вот метод независимых компонент поможет решить данную задачу. Математически постановка выглядит следующим образом. Представим одну поступающую смесь в виде линейной комбинации (1), где а — так называемые коэффициенты смещения, а s — значения вектора независимых компонент. То при определенном наборе поступающих входных сигналов выражение можно представить в матричном виде (2), где Х — матрица значений входных сигналов, А — матрица коэффициентов смещения (на английском часто называемая как mixing matrix), S — матрица независимых компонент.

Так вот что позволяет сделать метод независимых компонент: при наличии известных значений только матрицы Х, метод ищет значения матрицы S, которая представляет собой набор независимых компонент, описывающих наши независимые сигналы, и такие значения матрицы А, с помощью которых можно перейти из пространства S в пространство X (и соответственно наоборот). Конечная постановка обычно записывается так:

Обратная матрица А в английской литературе часто называют как unmixing matrix или demixing matrix и обычно обозначают как символом W.

Работа метода основана на двух принципах или обязательных условиях:

• Независимые компоненты обязательно должны быть статистически независимыми (значения матрицы S). Грубо говоря, значения одного вектора независимой компоненты никак не влияет на значения другой компоненты.
• Независимые компоненты обязательно должны иметь негауссово распределение.

Стоит также сказать, что многие хитрецы часто используют данный метод для решения задачи понижения размерности данных в Machine Learning, то есть используют как аналог Метода главных компонент (Principal component analysis, PCA). Идея рискованная, но иногда срабатывает.

Существует довольно много алгоритмов, которые реализуют рассматриваемый метод независимых компонент, например, Infomax, KernelICA, JADE, FastICA. Разные алгоритмы основаны на разных идеях, но если грубо округлить, то в основе работы лежат такие приемы, как «отбеливание» векторов, минимизация значений корреляции и минимизация «взаимной информации» (через информационную энтропию) между компонентами, максимизация негауссовости и т.д. За более подробной информацией следует обратиться к специализированной литературе, например к такой: URL .

В данной статье мы рассмотрим простой пример практическое применение алгоритма FastICA для разделения смеси из двух искусственных сигналов на языке Python с использованием готовой реализации алгоритма в известной библиотеке sklearn.

И так, для работы нам понадобятся следующие библиотеки: numpy, matplotlib и sklearn. На Linux все это дело легко устанавливается через пакетный менеджер apt-get или pip. Проще всего сделать примерно так:

Для Windows можно скачать готовую сборку Python под названием Anaconda, которая уже включает в себя все нужные библиотеки.

Сразу приведу ссылку на небольшой скрипт, который я написал для тестов: ссылка

Скрипт генерирует два разных по форме сигнала с шумом, из которых создается две смеси, которые как бы воспринимают два наших микрофона. Ниже приведен график исходных сигналов источников и график для тех сигналов, которые воспринимают микрофоны (графики смесей).

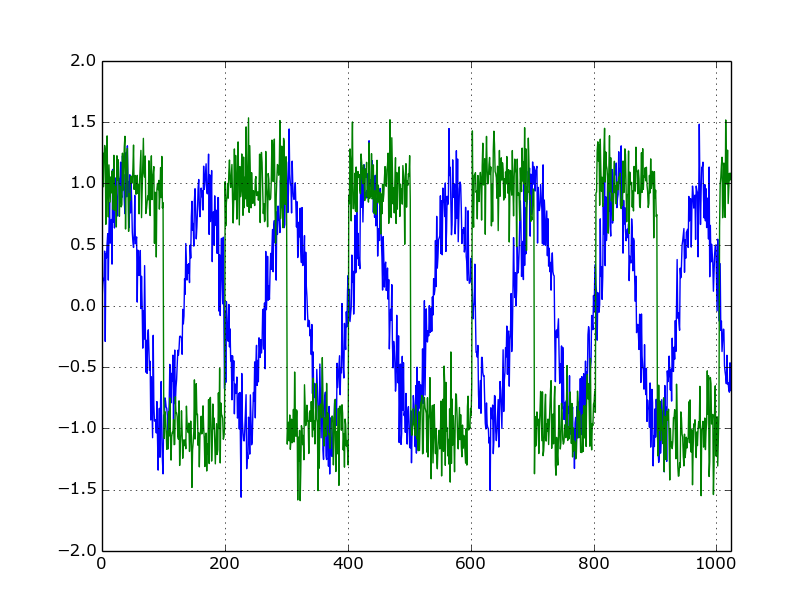
Сигналы от источников:

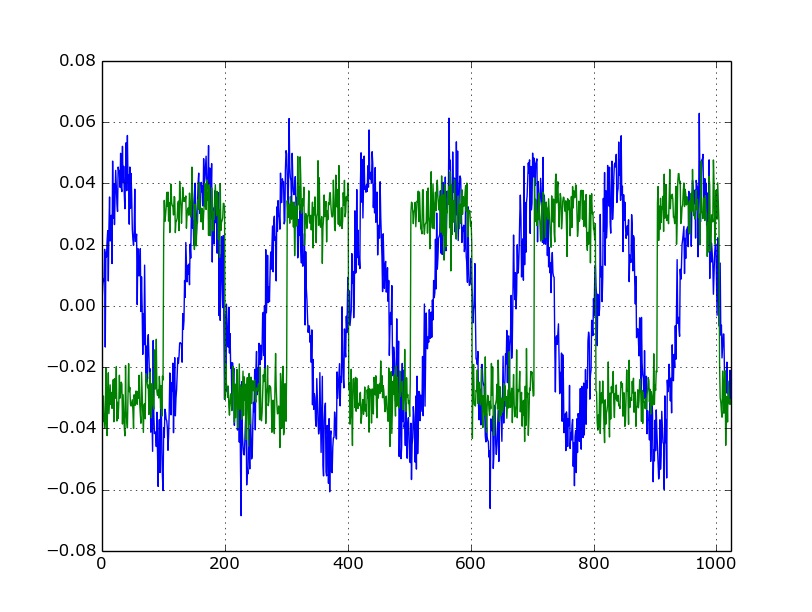
Смешанные сигналы (пусть синий сигнал - так воспринимает микрофон 1, зеленый - так воспринимает микрофон 2):

Далее микстуры прогоняются через FastICA алгоритм, на выходе которого мы получаем матрицу независимых компонент S.
Некоторые особенности работы FastICA в sklearn:

• Исходные данные необходимо подавать в определенном виде, а именно строки представляют собой значения входных векторов, а количество столбцов должны быть равны числу входных векторов. Например, у нас на вход идут 2 сигнала по 1024 отчета, поэтому входной массив для FastICA должен иметь размерность 1024х2.
• В данной библиотеке требуется указывать количество выделяемых алгоритмом независимых компонент. В случае если имеется априорная информация о численности компонент, то хорошо. Если неизвестно, то обычно число компонент приравнивают количеству входных векторов смесей. В нашем случае на вход поступает два коктейля, поэтому указываем число извлекаемых компонент равное двум.

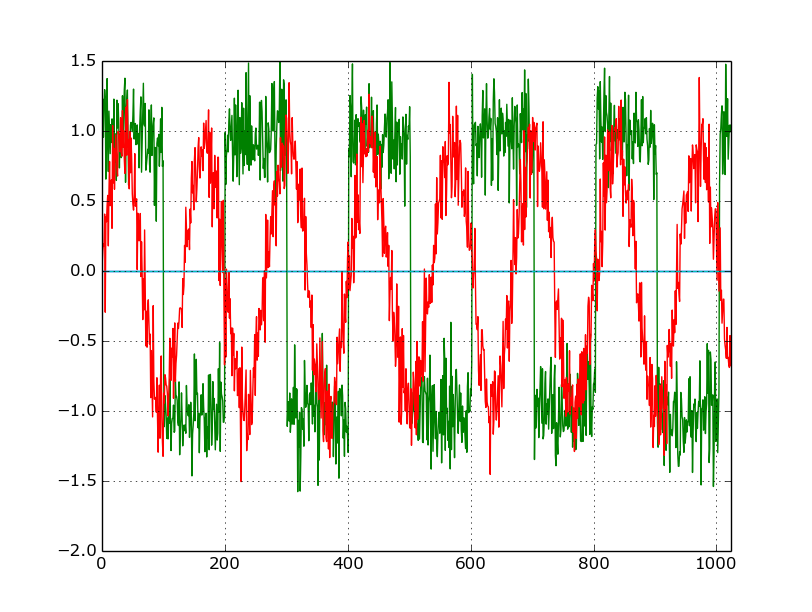
Вот так выглядит график матрицы независимых компонент S (результат работы FastICA):

Из данной матрицы S, по идее, можно получить наши исходные сигналы, умножив её на mixing матрицу А (следуя из формулы 2), что мы и делаем с помощью удобной библиотеки numpy. В результате получаем выделенные с помощью алгоритма FastICA сигналы источников, как показано на рисунке ниже.

Алгоритм в данной библиотеке работает не всегда точно, потому что матрицы A и S изначально заполняются случайными числами, от чего зависит скорость и точность работы.

Также на сайте с документацией sklearn есть похожий пример по Blind Source Separetion с использованием ICA и PCA, вот URL.

И еще раз, ссылка на скрипт, который был написан для данной статьи: https://gist.github.com/Tetraquark/5bf052134d413f79748ce3aceaaf42df